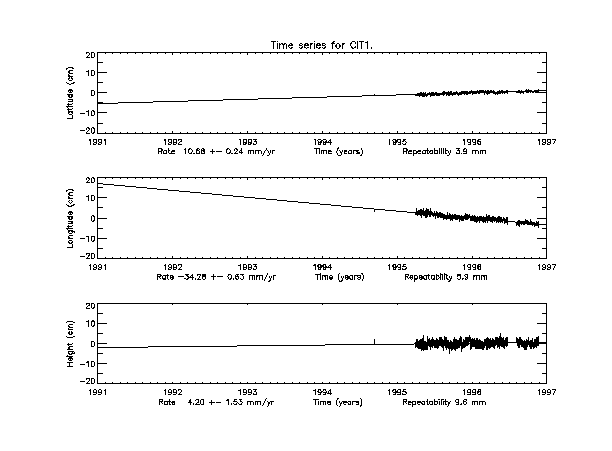
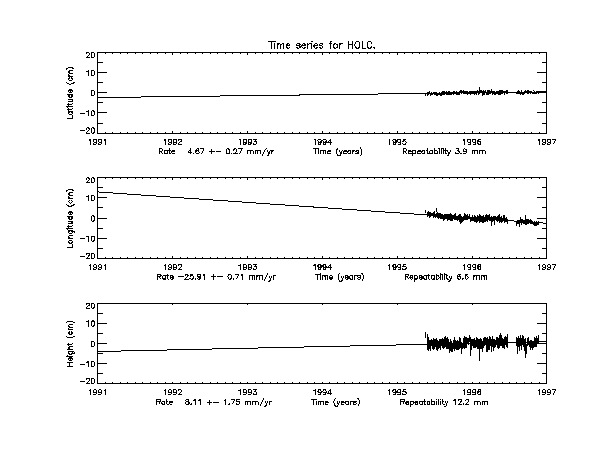
Required skills
- Knowledge of geometry and trigonometry (Pythagorean theorem,
trigonometric functions)
- Ability to do dimensional analysis
- Reading a graph
Background
If you live in Southern California, you are well aware of the numerous
earthquakes that the region experiences every year, even every day.
Most of these earthquakes are too small to feel, but every now and
again there is a major earthquake, like Landers ( 1992) or Northridge
( 1994. ) These earthquakes occur as a result of complex tectonic
processes that are responsible for the increasing movement of Los
Angeles toward San Francisco.
California is the location of a transform boundary between two plates,
the continental North American plate and the oceanic Pacific plate.
The most famous surface expression of this boundary is the San Andreas
fault. As these two plates grind slowly past each other, they create
massive strain in the crust, which is released in the form of earthquakes.
The San Andreas is a broad fault zone that allows the release of the
strain which accumulates along the boundary. [Link to figure: CA,
with plates and San Andreas identified]
To complicate matters even more, Los Angeles is located near a place
on the San Andreas where things become very complex. If you look at
a map of Southern California and locate the San Andreas fault (a
linear feature along which many highways run parallel,) you can
see that the fault makes a left bend right around Los Angeles. This
causes a lot of strain to build up in the LA area, because it is very
difficult for the two plates to move past each other around that bend.
In order to relieve the strain, the earth's crust reacts much differently
than in other areas on the San Andreas. [Link to figure: close-up
of So Cal, with plates, San Andreas, left bend, and LA identified]
This explains the reason why the Los Angeles and surrounding basins'
fault systems are so complex. In the LA area, much of the strain built
up by North America and the Pacific plates sliding past each other
is relieved by a series of thrust faults, which are responsible for
creating many of the mountain ranges and hills in the area. [Link
to figure: thrust fault model, how mtns are built] The San Gabriel
Mountains are a good example of this. Several thrust faults are responsible
for the uplift of these mountains, but for the purposes of this exercise,
we will assume that the Sierra Madre fault, located at the base of
the San Gabriels, is solely responsible for the uplift of these mountains.[Link
to figure: satellite image of LA basin, with topography apparent,
San Gabes and Sierra Madre identified]
Helpful Formulas
- Pythagorean theorem: D = (Dx2 + Dy2)1/2
- Dx = Latitude rate
- Dy = Longitude rate
- D = Horizontal rate
- Difference in Rates:
- 1) Rate for movement in latitudeHOLC - Rate for movement in latitude
CIT1
- 2) Rate for movement in longitudeHOLC - Rate for movement in longitude
CIT1
- Trigonometric functions: sin q = opposite side / hypotenuse
- cos q = adjacent side / hypotenuse
- tan q = opposite side /hypotenuse
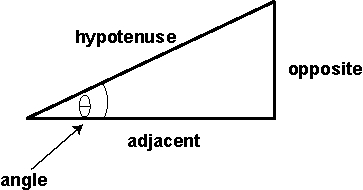
Procedure
1. Obtain a print-out of the time series for HOLC and CIT1.
2. Take the difference between the rates for the latitude and longitude
for each station.
3. Using the Pythagorean theorem and the values you just calculated,
solve for the resultant vector, which equals the horizontal rate.
(Note: positive values are for north and east, negative values
for south and west)
4. Assume that the San Gabriels have grown as a result of movement
on the Sierra Madre thrust fault only; and that the Sierra Madre fault
is dipping 45ƒ. Use trigonometry to solve for the hypotenuse, which
equals the motion along the fault.
5. Using the rate on the Sierra Madre that you calculated in Step
4, calculate the approximate number of earthquakes it took to build
the San Gabriel Mountains. Assume that the mountains have grown only
in M = 7.5 events (in a M = 7.5 event, there is 7 m of dip-slip
motion on a 65 x 20 km rupture surface on the fault;) the elevation
of the San Gabriels is 1500 m and the recurrence interval is 3000
years.
6. How does the number you calculated in Step 5 change if the fault
only experiences M = 5.0 earthquakes, which have 10 cm of dip-slip
movement on a 4 x 4 km rupture surface?
Questions to Answer
- How would erosion effect these calculations?
- How would a change in the dip angle effect these calculations?
- Why do we take the difference of the rates of the two stations?
- What is the difference between the growth of the San Gabriels
in M=7.5 events vs. M=5.0 events?

